Cilindro: Cuerpo geométrico formado por una superficie lateral curva y cerrada y dos planos paralelos que forman sus bases, superficie que se forma cuando una recta, llamada generatriz gira alrededor de otra recta paralela, eje. Otra forma de definirlo es el cuerpo que se genera cuando un Rectángulo gira alrededor de uno de sus lados.
• Eje. Es el lado fijo alrededor del que gira el rectángulo
• Bases. Son aquellos círculos que crean los lados perpendiculares al eje
• Generatriz. Es el lado que engendra el cilindro, opuesto al eje. La generatriz del cilindro es igual a la altura.
• Altura. Es la distancia entre las bases y es igual a la generatriz.

Un cilindro puede ser
• Cilindro rectangular: si el eje del cilindro es perpendicular a las bases 

• Cilindro oblicuo: si el eje no es perpendicular a las bases 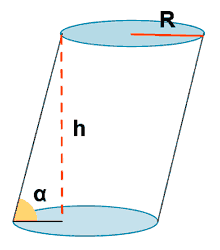

• Cilindro de revolución: si está limitado por una superficie cilíndrica de revolución. 




Es el cuerpo de revolución obtenido al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
Elementos de Un Cono
- Base (B): es la cara plana inferior del cono, que en el caso del cono circular recto, es un círculo cuyo radio es uno de los catetos del triángulo generador.
- Altura (h): distancia del plano de la base al vértice de la pirámide.
- Vértice (V): punto donde confluyen las infinitas generatrices.
- Generatriz (g): Línea que al girar sobre el eje del cono engendra la superficie cónica de revolución.
- Superficie generatriz (Sg):en el cono recto de revolución,es el triángulo rectángulo que lo engendra al girar 360° sobre uno de sus catetos, que es el eje de rotación y, que es a su vez, la altura del cono. El otro cateto es el radio de la base. La hipotenusa la generatriz (g).
Volumen Del Cono
Con
recipientes de forma cilíndrica o cónica es posible comparar su volumen. De
esta manera, es posible verificar que el volumen del cono es 1/3 del volumen de
un cilindro que tiene la misma base y la misma altura. Por lo tanto el volumen
del conoce puede calcular con la fórmula:
LA ESFERA
Elemento
|
Ejemplo
|
Esfera:
La esfera es
el espacio geométrico de puntos que equidistan a un mismo punto que se
denomina centro. El radio es la distancia entre el centro y un punto de la
esfera, y se denota r.
|
|
Semiesfera:
Es cada una
de las partes en que queda dividida la superficie esférica por un plano que
pasa por el centro de la esfera, llamado plano diametral. También se le
conoce como hemisferio.
|
|
Huso esférico:
El huso esférico es la parte de la superficie de una esfera
comprendida entre dos planos que se cortan en el diámetro de aquella.
|
|
Casquete esférico:
Un casquete
esférico es cada una de las partes de la esfera determinada por un plano
secante.
|
|
Zona esférica:
Una zona
esférica es la parte de la esfera comprendida entre dos planos secantes paralelos.
|
|
1. La cúpula de
una catedral tiene forma semiesférica, de radio 50 m. Si restaurarla tiene un
costo de 300 € el m2, ¿A cuánto ascenderá el presupuesto de la restauración?
Solución:
1.
Calcular el área
Necesitaremos la fórmula del área
A = 2 π r2
A = 2 π (50m)2
A = 15707, 96 m2
2.
Calcular el costo
Para calcular el importe total, el área que necesita restaurarse
se tiene que multiplicar por lo que cuesta restaurar cada metro cuadrado
Precio de restauración = 15.707,96 m2 * 300 €
Precio de restauración = 4.712.388,98 €



























No hay comentarios.:
Publicar un comentario