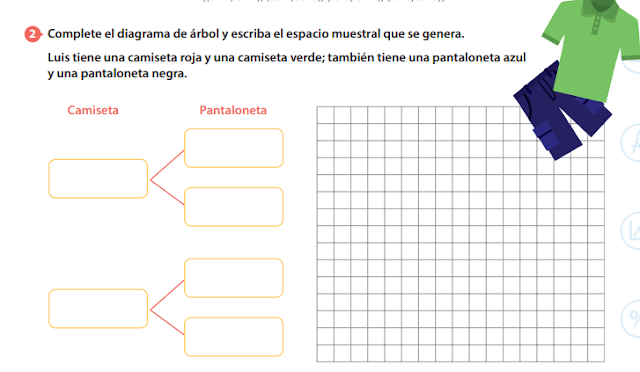
Diagrama de Árbol
 es una herramienta que se utiliza para determinar si en realidad en el cálculo de muchas opciones se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de árbol.
es una herramienta que se utiliza para determinar si en realidad en el cálculo de muchas opciones se requiere conocer el número de objetos que forman parte del espacio muestral, estos se pueden determinar con la construcción de un diagrama de árbol.
El diagrama de árbol es una representación gráfica de los posibles resultados del experimento, el cual consta de una serie de pasos, donde cada uno de estos tiene un número infinito de maneras de ser llevado a cabo. Se utiliza en los problemas de conteo y probabilidad.
El espacio muestral del experimento que consiste en lanzar dos monedas simultáneamente, se puede escribir a
partir del diagrama de árbol.
S = {(cara, cara); (cara, sello); (sello, cara); (sello, sello)}- Ejemplos
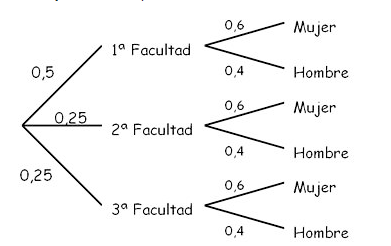
Una universidad está formada por tres facultades:
- La 1ª con el 50% de estudiantes.
- La 2ª con el 25% de estudiantes.
- La 3ª con el 25% de estudiantes.
Las mujeres están repartidas uniformemente, siendo un 60% del total en cada facultad.
El taller esta En classroom
FACTORIAL
El factorial de un entero positivo se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta "n".
Se representa:
La operación de factorial aparece en muchas áreas de las matemáticas, particularmente en combinatoria y análisis matemático. De manera fundamental el factorial de n representa el número de formas distintas de ordenar n objetos distintos (elementos sin repetición).
Si tenemos por ejemplo un número n, que represente un número natural mayor que 1, lo llamaremos factorial de n y lo representaremos como n!, al producto de los n número no nulos que aparecen primero. Con esto lo que queremos decir es que un número factorial es el producto de varios números naturales siguientes a partir de uno. Entonces para todo número natural n, se denomina factorial o factorial de n al producto de todos los números naturales desde 1 hasta n. Observemos el siguiente ejemplo:
0! se lee cero factorial
Por ejemplo: 4! se lee cuatro factorial y se resuelve así:
4! = 1 x 2 x 3 x 4 se multiplica todos los números
4! = 24
Propiedad: Hay que tener en cuenta la siguiente propiedad de números factoriales
n! = (n-1)! x n donde n = 3
3! = ( 3 - 1 )! x 3
3! = ( 2 )! x 3
3! = 2 x 3
3! = 6
Ahora hallaremos los siguientes factoriales:
Reducir un Factorial:
7! * 8 = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
7! * 8 = 8!
Expresar 6! en 5!
6! = 1 x 2 x 3 x 4 x 5 x 6
6! = 5! x 6
Otro ejemplo:
Otro Ejemplo
Doble factorial
Se define el doble factorial de n mediante la relación de recurrencia:
Por ejemplo:
El doble factorial de un número negativo par no está definido.
Algunas identidades de los dobles factoriales:
Actividad 2 esta en classroom